Welcome to the world of state area fashions. On this world, there’s a latent course of, hidden from our eyes; and there are observations we make concerning the issues it produces. The method evolves attributable to some hidden logic (transition mannequin); and the way in which it produces the observations follows some hidden logic (remark mannequin). There may be noise in course of evolution, and there may be noise in remark. If the transition and remark fashions each are linear, and the method in addition to remark noise are Gaussian, now we have a linear-Gaussian state area mannequin (SSM). The duty is to deduce the latent state from the observations. Essentially the most well-known approach is the Kálmán filter.
In sensible purposes, two traits of linear-Gaussian SSMs are particularly engaging.
For one, they allow us to estimate dynamically altering parameters. In regression, the parameters may be considered as a hidden state; we might thus have a slope and an intercept that change over time. When parameters can range, we communicate of dynamic linear fashions (DLMs). That is the time period we’ll use all through this submit when referring to this class of fashions.
Second, linear-Gaussian SSMs are helpful in time-series forecasting as a result of Gaussian processes may be added. A time collection can thus be framed as, e.g. the sum of a linear development and a course of that varies seasonally.
Utilizing tfprobability, the R wrapper to TensorFlow Likelihood, we illustrate each facets right here. Our first instance will probably be on dynamic linear regression. In an in depth walkthrough, we present on how one can match such a mannequin, how one can acquire filtered, in addition to smoothed, estimates of the coefficients, and how one can acquire forecasts.
Our second instance then illustrates course of additivity. This instance will construct on the primary, and may function a fast recap of the general process.
Let’s leap in.
Dynamic linear regression instance: Capital Asset Pricing Mannequin (CAPM)
Our code builds on the just lately launched variations of TensorFlow and TensorFlow Likelihood: 1.14 and 0.7, respectively.
Be aware how there’s one factor we used to do recently that we’re not doing right here: We’re not enabling keen execution. We are saying why in a minute.
Our instance is taken from Petris et al.(2009)(Petris, Petrone, and Campagnoli 2009), chapter 3.2.7.
Apart from introducing the dlm package deal, this e book supplies a pleasant introduction to the concepts behind DLMs usually.
For instance dynamic linear regression, the authors characteristic a dataset, initially from Berndt(1991)(Berndt 1991) that has month-to-month returns, collected from January 1978 to December 1987, for 4 totally different shares, the 30-day Treasury Invoice – standing in for a risk-free asset –, and the value-weighted common returns for all shares listed on the New York and American Inventory Exchanges, representing the general market returns.
Let’s have a look.
# As the info doesn't appear to be obtainable on the deal with given in Petris et al. any extra,
# we put it on the weblog for obtain
# obtain from:
# https://github.com/rstudio/tensorflow-blog/blob/grasp/docs/posts/2019-06-25-dynamic_linear_models_tfprobability/knowledge/capm.txt"
df <- read_table(
"capm.txt",
col_types = record(X1 = col_date(format = "%Y.%m"))) %>%
rename(month = X1)
df %>% glimpse()Observations: 120
Variables: 7
$ month <date> 1978-01-01, 1978-02-01, 1978-03-01, 1978-04-01, 1978-05-01, 19…
$ MOBIL <dbl> -0.046, -0.017, 0.049, 0.077, -0.011, -0.043, 0.028, 0.056, 0.0…
$ IBM <dbl> -0.029, -0.043, -0.063, 0.130, -0.018, -0.004, 0.092, 0.049, -0…
$ WEYER <dbl> -0.116, -0.135, 0.084, 0.144, -0.031, 0.005, 0.164, 0.039, -0.0…
$ CITCRP <dbl> -0.115, -0.019, 0.059, 0.127, 0.005, 0.007, 0.032, 0.088, 0.011…
$ MARKET <dbl> -0.045, 0.010, 0.050, 0.063, 0.067, 0.007, 0.071, 0.079, 0.002,…
$ RKFREE <dbl> 0.00487, 0.00494, 0.00526, 0.00491, 0.00513, 0.00527, 0.00528, …df %>% collect(key = "image", worth = "return", -month) %>%
ggplot(aes(x = month, y = return, coloration = image)) +
geom_line() +
facet_grid(rows = vars(image), scales = "free")
Determine 1: Month-to-month returns for chosen shares; knowledge from Berndt (1991).
The Capital Asset Pricing Mannequin then assumes a linear relationship between the surplus returns of an asset below research and the surplus returns of the market. For each, extra returns are obtained by subtracting the returns of the chosen risk-free asset; then, the scaling coefficient between them reveals the asset to both be an “aggressive” funding (slope > 1: adjustments available in the market are amplified), or a conservative one (slope < 1: adjustments are damped).
Assuming this relationship doesn’t change over time, we will simply use lm for instance this. Following Petris et al. in zooming in on IBM because the asset below research, now we have
Name:
lm(system = ibm ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.11850 -0.03327 -0.00263 0.03332 0.15042
Coefficients:
Estimate Std. Error t worth Pr(>|t|)
(Intercept) -0.0004896 0.0046400 -0.106 0.916
x 0.4568208 0.0675477 6.763 5.49e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual commonplace error: 0.05055 on 118 levels of freedom
A number of R-squared: 0.2793, Adjusted R-squared: 0.2732
F-statistic: 45.74 on 1 and 118 DF, p-value: 5.489e-10So IBM is discovered to be a conservative funding, the slope being ~ 0.5. However is that this relationship secure over time?
Let’s flip to tfprobability to research.
We need to use this instance to reveal two important purposes of DLMs: acquiring smoothing and/or filtering estimates of the coefficients, in addition to forecasting future values. So not like Petris et al., we divide the dataset right into a coaching and a testing half:.
We now assemble the mannequin. sts_dynamic_linear_regression() does what we wish:
We cross it the column of extra market returns, plus a column of ones, following Petris et al.. Alternatively, we might middle the one predictor – this is able to work simply as nicely.
How are we going to coach this mannequin? Technique-wise, now we have a alternative between variational inference (VI) and Hamiltonian Monte Carlo (HMC). We’ll see each. The second query is: Are we going to make use of graph mode or keen mode? As of at this time, for each VI and HMC, it’s most secure – and quickest – to run in graph mode, so that is the one approach we present. In just a few weeks, or months, we must always be capable to prune lots of sess$run()s from the code!
Usually in posts, when presenting code we optimize for straightforward experimentation (which means: line-by-line executability), not modularity. This time although, with an essential variety of analysis statements concerned, it’s best to pack not simply the becoming, however the smoothing and forecasting as nicely right into a operate (which you possibly can nonetheless step by way of for those who needed). For VI, we’ll have a match _with_vi operate that does all of it. So once we now begin explaining what it does, don’t sort within the code simply but – it’ll all reappear properly packed into that operate, so that you can copy and execute as a complete.
Becoming a time collection with variational inference
Becoming with VI just about appears like coaching historically used to look in graph-mode TensorFlow. You outline a loss – right here it’s accomplished utilizing sts_build_factored_variational_loss() –, an optimizer, and an operation for the optimizer to cut back that loss:
optimizer <- tf$compat$v1$prepare$AdamOptimizer(0.1)
# solely prepare on the coaching set!
loss_and_dists <- ts_train %>% sts_build_factored_variational_loss(mannequin = mannequin)
variational_loss <- loss_and_dists[[1]]
train_op <- optimizer$decrease(variational_loss)Be aware how the loss is outlined on the coaching set solely, not the entire collection.
Now to truly prepare the mannequin, we create a session and run that operation:
with (tf$Session() %as% sess, {
sess$run(tf$compat$v1$global_variables_initializer())
for (step in 1:n_iterations) {
res <- sess$run(train_op)
loss <- sess$run(variational_loss)
if (step %% 10 == 0)
cat("Loss: ", as.numeric(loss), "n")
}
})Given now we have that session, let’s make use of it and compute all of the estimates we want.
Once more, – the next snippets will find yourself within the fit_with_vi operate, so don’t run them in isolation simply but.
Acquiring forecasts
The very first thing we wish for the mannequin to present us are forecasts. With a view to create them, it wants samples from the posterior. Fortunately we have already got the posterior distributions, returned from sts_build_factored_variational_loss, so let’s pattern from them and cross them to sts_forecast:
sts_forecast() returns distributions, so we name tfd_mean() to get the posterior predictions and tfd_stddev() for the corresponding commonplace deviations:
fc_means <- forecast_dists %>% tfd_mean()
fc_sds <- forecast_dists %>% tfd_stddev()By the way in which – as now we have the complete posterior distributions, we’re on no account restricted to abstract statistics! We might simply use tfd_sample() to acquire particular person forecasts.
Smoothing and filtering (Kálmán filter)
Now, the second (and final, for this instance) factor we’ll need are the smoothed and filtered regression coefficients. The well-known Kálmán Filter is a Bayesian-in-spirit technique the place at every time step, predictions are corrected by how a lot they differ from an incoming remark. Filtering estimates are primarily based on observations we’ve seen to this point; smoothing estimates are computed “in hindsight,” making use of the entire time collection.
We first create a state area mannequin from our time collection definition:
# solely do that on the coaching set
# returns an occasion of tfd_linear_gaussian_state_space_model()
ssm <- mannequin$make_state_space_model(size(ts_train), param_vals = posterior_samples)tfd_linear_gaussian_state_space_model(), technically a distribution, supplies the Kálmán filter functionalities of smoothing and filtering.
To acquire the smoothed estimates:
c(smoothed_means, smoothed_covs) %<-% ssm$posterior_marginals(ts_train)And the filtered ones:
c(., filtered_means, filtered_covs, ., ., ., .) %<-% ssm$forward_filter(ts_train)Lastly, we have to consider all these.
Placing all of it collectively (the VI version)
So right here’s the entire operate, fit_with_vi, prepared for us to name.
fit_with_vi <-
operate(ts,
ts_train,
mannequin,
n_iterations,
n_param_samples,
n_forecast_steps,
n_forecast_samples) {
optimizer <- tf$compat$v1$prepare$AdamOptimizer(0.1)
loss_and_dists <-
ts_train %>% sts_build_factored_variational_loss(mannequin = mannequin)
variational_loss <- loss_and_dists[[1]]
train_op <- optimizer$decrease(variational_loss)
with (tf$Session() %as% sess, {
sess$run(tf$compat$v1$global_variables_initializer())
for (step in 1:n_iterations) {
sess$run(train_op)
loss <- sess$run(variational_loss)
if (step %% 1 == 0)
cat("Loss: ", as.numeric(loss), "n")
}
variational_distributions <- loss_and_dists[[2]]
posterior_samples <-
Map(
operate(d)
d %>% tfd_sample(n_param_samples),
variational_distributions %>% reticulate::py_to_r() %>% unname()
)
forecast_dists <-
ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)
fc_means <- forecast_dists %>% tfd_mean()
fc_sds <- forecast_dists %>% tfd_stddev()
ssm <- mannequin$make_state_space_model(size(ts_train), param_vals = posterior_samples)
c(smoothed_means, smoothed_covs) %<-% ssm$posterior_marginals(ts_train)
c(., filtered_means, filtered_covs, ., ., ., .) %<-% ssm$forward_filter(ts_train)
c(posterior_samples, fc_means, fc_sds, smoothed_means, smoothed_covs, filtered_means, filtered_covs) %<-%
sess$run(record(posterior_samples, fc_means, fc_sds, smoothed_means, smoothed_covs, filtered_means, filtered_covs))
})
record(
variational_distributions,
posterior_samples,
fc_means[, 1],
fc_sds[, 1],
smoothed_means,
smoothed_covs,
filtered_means,
filtered_covs
)
}And that is how we name it.
# variety of VI steps
n_iterations <- 300
# pattern dimension for posterior samples
n_param_samples <- 50
# pattern dimension to attract from the forecast distribution
n_forecast_samples <- 50
# this is the mannequin once more
mannequin <- ts %>%
sts_dynamic_linear_regression(design_matrix = cbind(rep(1, size(x)), x) %>% tf$solid(tf$float32))
# name fit_vi outlined above
c(
param_distributions,
param_samples,
fc_means,
fc_sds,
smoothed_means,
smoothed_covs,
filtered_means,
filtered_covs
) %<-% fit_vi(
ts,
ts_train,
mannequin,
n_iterations,
n_param_samples,
n_forecast_steps,
n_forecast_samples
)Curious concerning the outcomes? We’ll see them in a second, however earlier than let’s simply rapidly look on the various coaching technique: HMC.
Placing all of it collectively (the HMC version)
tfprobability supplies sts_fit_with_hmc to suit a DLM utilizing Hamiltonian Monte Carlo. Latest posts (e.g., Hierarchical partial pooling, continued: Various slopes fashions with TensorFlow Likelihood) confirmed how one can arrange HMC to suit hierarchical fashions; right here a single operate does all of it.
Right here is fit_with_hmc, wrapping sts_fit_with_hmc in addition to the (unchanged) methods for acquiring forecasts and smoothed/filtered parameters:
num_results <- 200
num_warmup_steps <- 100
fit_hmc <- operate(ts,
ts_train,
mannequin,
num_results,
num_warmup_steps,
n_forecast,
n_forecast_samples) {
states_and_results <-
ts_train %>% sts_fit_with_hmc(
mannequin,
num_results = num_results,
num_warmup_steps = num_warmup_steps,
num_variational_steps = num_results + num_warmup_steps
)
posterior_samples <- states_and_results[[1]]
forecast_dists <-
ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)
fc_means <- forecast_dists %>% tfd_mean()
fc_sds <- forecast_dists %>% tfd_stddev()
ssm <-
mannequin$make_state_space_model(size(ts_train), param_vals = posterior_samples)
c(smoothed_means, smoothed_covs) %<-% ssm$posterior_marginals(ts_train)
c(., filtered_means, filtered_covs, ., ., ., .) %<-% ssm$forward_filter(ts_train)
with (tf$Session() %as% sess, {
sess$run(tf$compat$v1$global_variables_initializer())
c(
posterior_samples,
fc_means,
fc_sds,
smoothed_means,
smoothed_covs,
filtered_means,
filtered_covs
) %<-%
sess$run(
record(
posterior_samples,
fc_means,
fc_sds,
smoothed_means,
smoothed_covs,
filtered_means,
filtered_covs
)
)
})
record(
posterior_samples,
fc_means[, 1],
fc_sds[, 1],
smoothed_means,
smoothed_covs,
filtered_means,
filtered_covs
)
}
c(
param_samples,
fc_means,
fc_sds,
smoothed_means,
smoothed_covs,
filtered_means,
filtered_covs
) %<-% fit_hmc(ts,
ts_train,
mannequin,
num_results,
num_warmup_steps,
n_forecast,
n_forecast_samples)Now lastly, let’s check out the forecasts and filtering resp. smoothing estimates.
Forecasts
Placing all we’d like into one dataframe, now we have
smoothed_means_intercept <- smoothed_means[, , 1] %>% colMeans()
smoothed_means_slope <- smoothed_means[, , 2] %>% colMeans()
smoothed_sds_intercept <- smoothed_covs[, , 1, 1] %>% colMeans() %>% sqrt()
smoothed_sds_slope <- smoothed_covs[, , 2, 2] %>% colMeans() %>% sqrt()
filtered_means_intercept <- filtered_means[, , 1] %>% colMeans()
filtered_means_slope <- filtered_means[, , 2] %>% colMeans()
filtered_sds_intercept <- filtered_covs[, , 1, 1] %>% colMeans() %>% sqrt()
filtered_sds_slope <- filtered_covs[, , 2, 2] %>% colMeans() %>% sqrt()
forecast_df <- df %>%
choose(month, IBM) %>%
add_column(pred_mean = c(rep(NA, size(ts_train)), fc_means)) %>%
add_column(pred_sd = c(rep(NA, size(ts_train)), fc_sds)) %>%
add_column(smoothed_means_intercept = c(smoothed_means_intercept, rep(NA, n_forecast_steps))) %>%
add_column(smoothed_means_slope = c(smoothed_means_slope, rep(NA, n_forecast_steps))) %>%
add_column(smoothed_sds_intercept = c(smoothed_sds_intercept, rep(NA, n_forecast_steps))) %>%
add_column(smoothed_sds_slope = c(smoothed_sds_slope, rep(NA, n_forecast_steps))) %>%
add_column(filtered_means_intercept = c(filtered_means_intercept, rep(NA, n_forecast_steps))) %>%
add_column(filtered_means_slope = c(filtered_means_slope, rep(NA, n_forecast_steps))) %>%
add_column(filtered_sds_intercept = c(filtered_sds_intercept, rep(NA, n_forecast_steps))) %>%
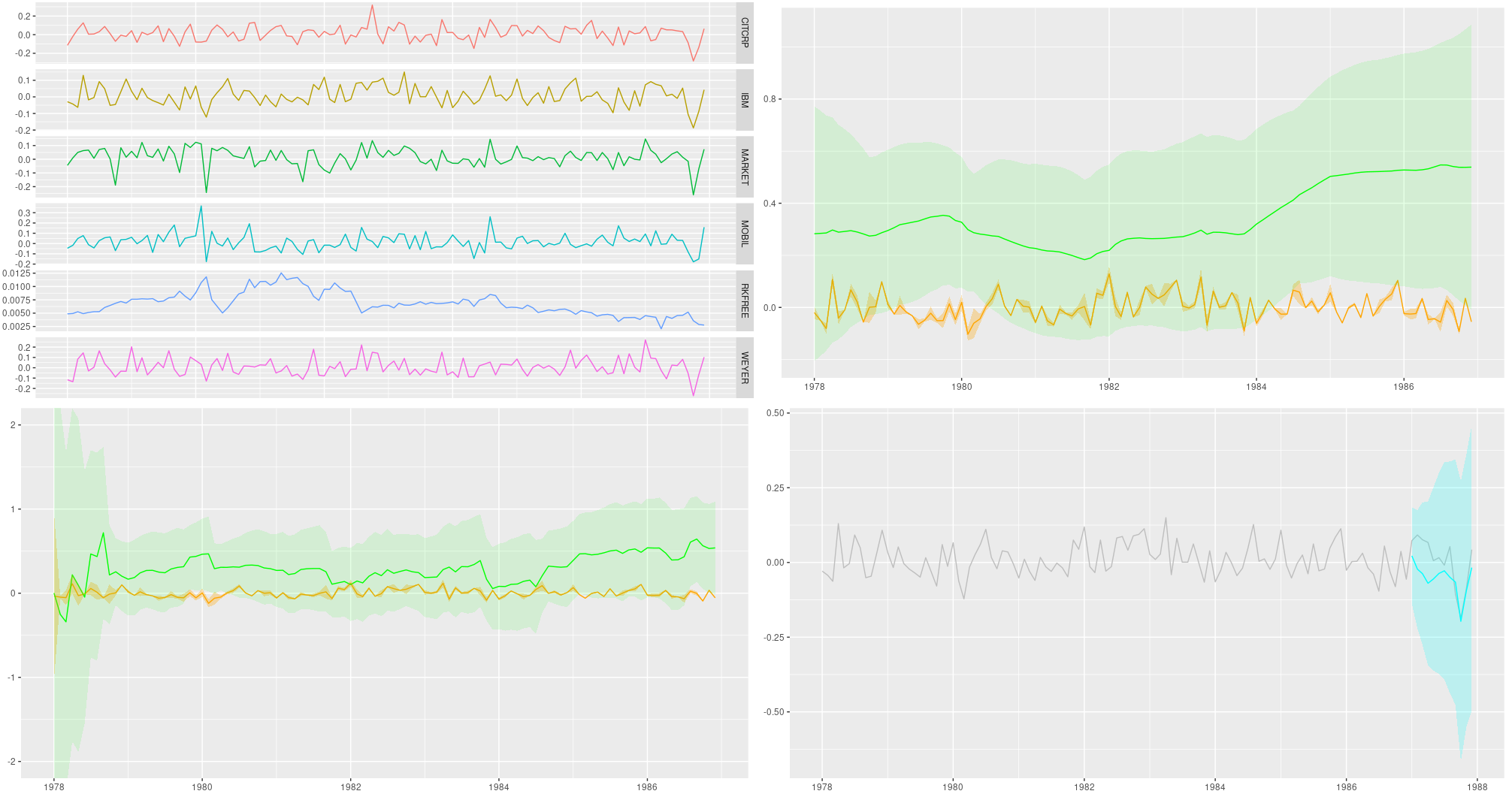
add_column(filtered_sds_slope = c(filtered_sds_slope, rep(NA, n_forecast_steps)))So right here first are the forecasts. We’re utilizing the estimates returned from VI, however we might simply as nicely have used these from HMC – they’re practically indistinguishable. The identical goes for the filtering and smoothing estimates displayed beneath.
ggplot(forecast_df, aes(x = month, y = IBM)) +
geom_line(coloration = "gray") +
geom_line(aes(y = pred_mean), coloration = "cyan") +
geom_ribbon(
aes(ymin = pred_mean - 2 * pred_sd, ymax = pred_mean + 2 * pred_sd),
alpha = 0.2,
fill = "cyan"
) +
theme(axis.title = element_blank())
Determine 2: 12-point-ahead forecasts for IBM; posterior means +/- 2 commonplace deviations.
Smoothing estimates
Listed below are the smoothing estimates. The intercept (proven in orange) stays fairly secure over time, however we do see a development within the slope (displayed in inexperienced).
ggplot(forecast_df, aes(x = month, y = smoothed_means_intercept)) +
geom_line(coloration = "orange") +
geom_line(aes(y = smoothed_means_slope),
coloration = "inexperienced") +
geom_ribbon(
aes(
ymin = smoothed_means_intercept - 2 * smoothed_sds_intercept,
ymax = smoothed_means_intercept + 2 * smoothed_sds_intercept
),
alpha = 0.3,
fill = "orange"
) +
geom_ribbon(
aes(
ymin = smoothed_means_slope - 2 * smoothed_sds_slope,
ymax = smoothed_means_slope + 2 * smoothed_sds_slope
),
alpha = 0.1,
fill = "inexperienced"
) +
coord_cartesian(xlim = c(forecast_df$month[1], forecast_df$month[length(ts) - n_forecast_steps])) +
theme(axis.title = element_blank())
Determine 3: Smoothing estimates from the Kálmán filter. Inexperienced: coefficient for dependence on extra market returns (slope), orange: vector of ones (intercept).
Filtering estimates
For comparability, listed below are the filtering estimates. Be aware that the y-axis extends additional up and down, so we will seize uncertainty higher:
ggplot(forecast_df, aes(x = month, y = filtered_means_intercept)) +
geom_line(coloration = "orange") +
geom_line(aes(y = filtered_means_slope),
coloration = "inexperienced") +
geom_ribbon(
aes(
ymin = filtered_means_intercept - 2 * filtered_sds_intercept,
ymax = filtered_means_intercept + 2 * filtered_sds_intercept
),
alpha = 0.3,
fill = "orange"
) +
geom_ribbon(
aes(
ymin = filtered_means_slope - 2 * filtered_sds_slope,
ymax = filtered_means_slope + 2 * filtered_sds_slope
),
alpha = 0.1,
fill = "inexperienced"
) +
coord_cartesian(ylim = c(-2, 2),
xlim = c(forecast_df$month[1], forecast_df$month[length(ts) - n_forecast_steps])) +
theme(axis.title = element_blank())
Determine 4: Filtering estimates from the Kálmán filter. Inexperienced: coefficient for dependence on extra market returns (slope), orange: vector of ones (intercept).
Up to now, we’ve seen a full instance of time-series becoming, forecasting, and smoothing/filtering, in an thrilling setting one doesn’t encounter too usually: dynamic linear regression. What we haven’t seen as but is the additivity characteristic of DLMs, and the way it permits us to decompose a time collection into its (theorized) constituents.
Let’s do that subsequent, in our second instance, anti-climactically making use of the iris of time collection, AirPassengers. Any guesses what elements the mannequin may presuppose?

Determine 5: AirPassengers.
Composition instance: AirPassengers
Libraries loaded, we put together the info for tfprobability:
The mannequin is a sum – cf. sts_sum – of a linear development and a seasonal element:
linear_trend <- ts %>% sts_local_linear_trend()
month-to-month <- ts %>% sts_seasonal(num_seasons = 12)
mannequin <- ts %>% sts_sum(elements = record(month-to-month, linear_trend))Once more, we might use VI in addition to MCMC to coach the mannequin. Right here’s the VI method:
n_iterations <- 100
n_param_samples <- 50
n_forecast_samples <- 50
optimizer <- tf$compat$v1$prepare$AdamOptimizer(0.1)
fit_vi <-
operate(ts,
ts_train,
mannequin,
n_iterations,
n_param_samples,
n_forecast_steps,
n_forecast_samples) {
loss_and_dists <-
ts_train %>% sts_build_factored_variational_loss(mannequin = mannequin)
variational_loss <- loss_and_dists[[1]]
train_op <- optimizer$decrease(variational_loss)
with (tf$Session() %as% sess, {
sess$run(tf$compat$v1$global_variables_initializer())
for (step in 1:n_iterations) {
res <- sess$run(train_op)
loss <- sess$run(variational_loss)
if (step %% 1 == 0)
cat("Loss: ", as.numeric(loss), "n")
}
variational_distributions <- loss_and_dists[[2]]
posterior_samples <-
Map(
operate(d)
d %>% tfd_sample(n_param_samples),
variational_distributions %>% reticulate::py_to_r() %>% unname()
)
forecast_dists <-
ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)
fc_means <- forecast_dists %>% tfd_mean()
fc_sds <- forecast_dists %>% tfd_stddev()
c(posterior_samples,
fc_means,
fc_sds) %<-%
sess$run(record(posterior_samples,
fc_means,
fc_sds))
})
record(variational_distributions,
posterior_samples,
fc_means[, 1],
fc_sds[, 1])
}
c(param_distributions,
param_samples,
fc_means,
fc_sds) %<-% fit_vi(
ts,
ts_train,
mannequin,
n_iterations,
n_param_samples,
n_forecast_steps,
n_forecast_samples
)For brevity, we haven’t computed smoothed and/or filtered estimates for the general mannequin. On this instance, this being a sum mannequin, we need to present one thing else as an alternative: the way in which it decomposes into elements.
However first, the forecasts:
forecast_df <- df %>%
add_column(pred_mean = c(rep(NA, size(ts_train)), fc_means)) %>%
add_column(pred_sd = c(rep(NA, size(ts_train)), fc_sds))
ggplot(forecast_df, aes(x = month, y = n)) +
geom_line(coloration = "gray") +
geom_line(aes(y = pred_mean), coloration = "cyan") +
geom_ribbon(
aes(ymin = pred_mean - 2 * pred_sd, ymax = pred_mean + 2 * pred_sd),
alpha = 0.2,
fill = "cyan"
) +
theme(axis.title = element_blank())
Determine 6: AirPassengers, 12-months-ahead forecast.
A name to sts_decompose_by_component yields the (centered) elements, a linear development and a seasonal issue:
component_dists <-
ts_train %>% sts_decompose_by_component(mannequin = mannequin, parameter_samples = param_samples)
seasonal_effect_means <- component_dists[[1]] %>% tfd_mean()
seasonal_effect_sds <- component_dists[[1]] %>% tfd_stddev()
linear_effect_means <- component_dists[[2]] %>% tfd_mean()
linear_effect_sds <- component_dists[[2]] %>% tfd_stddev()
with(tf$Session() %as% sess, {
c(
seasonal_effect_means,
seasonal_effect_sds,
linear_effect_means,
linear_effect_sds
) %<-% sess$run(
record(
seasonal_effect_means,
seasonal_effect_sds,
linear_effect_means,
linear_effect_sds
)
)
})
components_df <- forecast_df %>%
add_column(seasonal_effect_means = c(seasonal_effect_means, rep(NA, n_forecast_steps))) %>%
add_column(seasonal_effect_sds = c(seasonal_effect_sds, rep(NA, n_forecast_steps))) %>%
add_column(linear_effect_means = c(linear_effect_means, rep(NA, n_forecast_steps))) %>%
add_column(linear_effect_sds = c(linear_effect_sds, rep(NA, n_forecast_steps)))
ggplot(components_df, aes(x = month, y = n)) +
geom_line(aes(y = seasonal_effect_means), coloration = "orange") +
geom_ribbon(
aes(
ymin = seasonal_effect_means - 2 * seasonal_effect_sds,
ymax = seasonal_effect_means + 2 * seasonal_effect_sds
),
alpha = 0.2,
fill = "orange"
) +
theme(axis.title = element_blank()) +
geom_line(aes(y = linear_effect_means), coloration = "inexperienced") +
geom_ribbon(
aes(
ymin = linear_effect_means - 2 * linear_effect_sds,
ymax = linear_effect_means + 2 * linear_effect_sds
),
alpha = 0.2,
fill = "inexperienced"
) +
theme(axis.title = element_blank())
Determine 7: AirPassengers, decomposition right into a linear development and a seasonal element (each centered).
Wrapping up
We’ve seen how with DLMs, there’s a bunch of fascinating stuff you are able to do – aside from acquiring forecasts, which in all probability would be the final objective in most purposes – : You possibly can examine the smoothed and the filtered estimates from the Kálmán filter, and you’ll decompose a mannequin into its posterior elements. A very engaging mannequin is dynamic linear regression, featured in our first instance, which permits us to acquire regression coefficients that change over time.
This submit confirmed how one can accomplish this with tfprobability. As of at this time, TensorFlow (and thus, TensorFlow Likelihood) is in a state of considerable inner adjustments, with wanting to turn into the default execution mode very quickly. Concurrently, the superior TensorFlow Likelihood growth crew are including new and thrilling options every single day. Consequently, this submit is snapshot capturing how one can finest accomplish these objectives now: In case you’re studying this just a few months from now, chances are high that what’s work in progress now could have turn into a mature technique by then, and there could also be sooner methods to achieve the identical objectives. On the charge TFP is evolving, we’re excited for the issues to return!
Berndt, R. 1991. The Follow of Econometrics. Addison-Wesley.
Murphy, Kevin. 2012. Machine Studying: A Probabilistic Perspective. MIT Press.
Petris, Giovanni, sonia Petrone, and Patrizia Campagnoli. 2009. Dynamic Linear Fashions with r. Springer.