It’s 2019; nobody doubts the effectiveness of deep studying in pc imaginative and prescient. Or pure language processing. With “regular,” Excel-style, a.okay.a. tabular information nonetheless, the state of affairs is totally different.
Principally there are two circumstances: One, you could have numeric information solely. Then, creating the community is simple, and all will probably be about optimization and hyperparameter search. Two, you could have a mixture of numeric and categorical information, the place categorical may very well be something from ordered-numeric to symbolic (e.g., textual content). On this latter case, with categorical information coming into the image, there may be an especially good thought you may make use of: embed what are equidistant symbols right into a high-dimensional, numeric illustration. In that new illustration, we will outline a distance metric that permits us to make statements like “biking is nearer to working than to baseball,” or “😃 is nearer to 😂 than to 😠.” When not coping with language information, this method is known as entity embeddings.
Good as this sounds, why don’t we see entity embeddings used on a regular basis? Nicely, making a Keras community that processes a mixture of numeric and categorical information used to require a little bit of an effort. With TensorFlow’s new characteristic columns, usable from R by a mixture of tfdatasets and keras, there’s a a lot simpler solution to obtain this. What’s extra, tfdatasets follows the favored recipes idiom to initialize, refine, and apply a characteristic specification %>%-style. And at last, there are ready-made steps for bucketizing a numeric column, or hashing it, or creating crossed columns to seize interactions.
This put up introduces characteristic specs ranging from a state of affairs the place they don’t exist: principally, the established order till very not too long ago. Think about you could have a dataset like that from the Porto Seguro automobile insurance coverage competitors the place among the columns are numeric, and a few are categorical. You wish to prepare a completely linked community on it, with all categorical columns fed into embedding layers. How will you do this? We then distinction this with the characteristic spec method, which makes issues loads simpler – particularly when there’s a variety of categorical columns.
In a second utilized instance, we show the usage of crossed columns on the rugged dataset from Richard McElreath’s rethinking bundle. Right here, we additionally direct consideration to some technical particulars which can be price figuring out about.
Mixing numeric information and embeddings, the pre-feature-spec method
Our first instance dataset is taken from Kaggle. Two years in the past, Brazilian automobile insurance coverage firm Porto Seguro requested contributors to foretell how probably it’s a automobile proprietor will file a declare based mostly on a mixture of traits collected throughout the earlier yr. The dataset is relatively massive – there are ~ 600,000 rows within the coaching set, with 57 predictors. Amongst others, options are named in order to point the kind of the info – binary, categorical, or steady/ordinal.
Whereas it’s frequent in competitions to attempt to reverse-engineer column meanings, right here we simply make use of the kind of the info, and see how far that will get us.
Concretely, this implies we wish to
- use binary options simply the way in which they’re, as zeroes and ones,
- scale the remaining numeric options to imply 0 and variance 1, and
- embed the explicit variables (every one by itself).
We’ll then outline a dense community to foretell goal, the binary end result. So first, let’s see how we may get our information into form, in addition to construct up the community, in a “guide,” pre-feature-columns method.
When loading libraries, we already use the variations we’ll want very quickly: Tensorflow 2 (>= beta 1), and the event (= Github) variations of tfdatasets and keras:
On this first model of making ready the info, we make our lives simpler by assigning totally different R sorts, based mostly on what the options signify (categorical, binary, or numeric qualities):
# downloaded from https://www.kaggle.com/c/porto-seguro-safe-driver-prediction/information
path <- "prepare.csv"
porto <- read_csv(path) %>%
choose(-id) %>%
# to acquire variety of distinctive ranges, later
mutate_at(vars(ends_with("cat")), issue) %>%
# to simply maintain them other than the non-binary numeric information
mutate_at(vars(ends_with("bin")), as.integer)
porto %>% glimpse()Observations: 595,212
Variables: 58
$ goal <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,…
$ ps_ind_01 <dbl> 2, 1, 5, 0, 0, 5, 2, 5, 5, 1, 5, 2, 2, 1, 5, 5,…
$ ps_ind_02_cat <fct> 2, 1, 4, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1,…
$ ps_ind_03 <dbl> 5, 7, 9, 2, 0, 4, 3, 4, 3, 2, 2, 3, 1, 3, 11, 3…
$ ps_ind_04_cat <fct> 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1,…
$ ps_ind_05_cat <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_06_bin <int> 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_07_bin <int> 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,…
$ ps_ind_08_bin <int> 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0,…
$ ps_ind_09_bin <int> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,…
$ ps_ind_10_bin <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_11_bin <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_12_bin <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_13_bin <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_14 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_15 <dbl> 11, 3, 12, 8, 9, 6, 8, 13, 6, 4, 3, 9, 10, 12, …
$ ps_ind_16_bin <int> 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0,…
$ ps_ind_17_bin <int> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_ind_18_bin <int> 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1,…
$ ps_reg_01 <dbl> 0.7, 0.8, 0.0, 0.9, 0.7, 0.9, 0.6, 0.7, 0.9, 0.…
$ ps_reg_02 <dbl> 0.2, 0.4, 0.0, 0.2, 0.6, 1.8, 0.1, 0.4, 0.7, 1.…
$ ps_reg_03 <dbl> 0.7180703, 0.7660777, -1.0000000, 0.5809475, 0.…
$ ps_car_01_cat <fct> 10, 11, 7, 7, 11, 10, 6, 11, 10, 11, 11, 11, 6,…
$ ps_car_02_cat <fct> 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1,…
$ ps_car_03_cat <fct> -1, -1, -1, 0, -1, -1, -1, 0, -1, 0, -1, -1, -1…
$ ps_car_04_cat <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 8, 0, 0, 0, 0, 9,…
$ ps_car_05_cat <fct> 1, -1, -1, 1, -1, 0, 1, 0, 1, 0, -1, -1, -1, 1,…
$ ps_car_06_cat <fct> 4, 11, 14, 11, 14, 14, 11, 11, 14, 14, 13, 11, …
$ ps_car_07_cat <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ ps_car_08_cat <fct> 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0,…
$ ps_car_09_cat <fct> 0, 2, 2, 3, 2, 0, 0, 2, 0, 2, 2, 0, 2, 2, 2, 0,…
$ ps_car_10_cat <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ ps_car_11_cat <fct> 12, 19, 60, 104, 82, 104, 99, 30, 68, 104, 20, …
$ ps_car_11 <dbl> 2, 3, 1, 1, 3, 2, 2, 3, 3, 2, 3, 3, 3, 3, 1, 2,…
$ ps_car_12 <dbl> 0.4000000, 0.3162278, 0.3162278, 0.3741657, 0.3…
$ ps_car_13 <dbl> 0.8836789, 0.6188165, 0.6415857, 0.5429488, 0.5…
$ ps_car_14 <dbl> 0.3708099, 0.3887158, 0.3472751, 0.2949576, 0.3…
$ ps_car_15 <dbl> 3.605551, 2.449490, 3.316625, 2.000000, 2.00000…
$ ps_calc_01 <dbl> 0.6, 0.3, 0.5, 0.6, 0.4, 0.7, 0.2, 0.1, 0.9, 0.…
$ ps_calc_02 <dbl> 0.5, 0.1, 0.7, 0.9, 0.6, 0.8, 0.6, 0.5, 0.8, 0.…
$ ps_calc_03 <dbl> 0.2, 0.3, 0.1, 0.1, 0.0, 0.4, 0.5, 0.1, 0.6, 0.…
$ ps_calc_04 <dbl> 3, 2, 2, 2, 2, 3, 2, 1, 3, 2, 2, 2, 4, 2, 3, 2,…
$ ps_calc_05 <dbl> 1, 1, 2, 4, 2, 1, 2, 2, 1, 2, 3, 2, 1, 1, 1, 1,…
$ ps_calc_06 <dbl> 10, 9, 9, 7, 6, 8, 8, 7, 7, 8, 8, 8, 8, 10, 8, …
$ ps_calc_07 <dbl> 1, 5, 1, 1, 3, 2, 1, 1, 3, 2, 2, 2, 4, 1, 2, 5,…
$ ps_calc_08 <dbl> 10, 8, 8, 8, 10, 11, 8, 6, 9, 9, 9, 10, 11, 8, …
$ ps_calc_09 <dbl> 1, 1, 2, 4, 2, 3, 3, 1, 4, 1, 4, 1, 1, 3, 3, 2,…
$ ps_calc_10 <dbl> 5, 7, 7, 2, 12, 8, 10, 13, 11, 11, 7, 8, 9, 8, …
$ ps_calc_11 <dbl> 9, 3, 4, 2, 3, 4, 3, 7, 4, 3, 6, 9, 6, 2, 4, 5,…
$ ps_calc_12 <dbl> 1, 1, 2, 2, 1, 2, 0, 1, 2, 5, 3, 2, 3, 0, 1, 2,…
$ ps_calc_13 <dbl> 5, 1, 7, 4, 1, 0, 0, 3, 1, 0, 3, 1, 3, 4, 3, 6,…
$ ps_calc_14 <dbl> 8, 9, 7, 9, 3, 9, 10, 6, 5, 6, 6, 10, 8, 3, 9, …
$ ps_calc_15_bin <int> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
$ ps_calc_16_bin <int> 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1,…
$ ps_calc_17_bin <int> 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1,…
$ ps_calc_18_bin <int> 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,…
$ ps_calc_19_bin <int> 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1,…
$ ps_calc_20_bin <int> 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0,…We break up off 25% for validation.
The one factor we wish to do to the information earlier than defining the community is scaling the numeric options. Binary and categorical options can keep as is, with the minor correction that for the explicit ones, we’ll really go the community the numeric illustration of the issue information.
Right here is the scaling.
train_means <- colMeans(x_train[sapply(x_train, is.double)]) %>% unname()
train_sds <- apply(x_train[sapply(x_train, is.double)], 2, sd) %>% unname()
train_sds[train_sds == 0] <- 0.000001
x_train[sapply(x_train, is.double)] <- sweep(
x_train[sapply(x_train, is.double)],
2,
train_means
) %>%
sweep(2, train_sds, "/")
x_test[sapply(x_test, is.double)] <- sweep(
x_test[sapply(x_test, is.double)],
2,
train_means
) %>%
sweep(2, train_sds, "/")When constructing the community, we have to specify the enter and output dimensionalities for the embedding layers. Enter dimensionality refers back to the variety of totally different symbols that “are available in”; in NLP duties this might be the vocabulary dimension whereas right here, it’s merely the variety of values a variable can take.
Output dimensionality, the capability of the inner illustration, can then be calculated based mostly on some heuristic. Beneath, we’ll comply with a well-liked rule of thumb that takes the sq. root of the dimensionality of the enter.
In order half one of many community, right here we construct up the embedding layers in a loop, every wired to the enter layer that feeds it:
# variety of ranges per issue, required to specify enter dimensionality for
# the embedding layers
n_levels_in <- map(x_train %>% select_if(is.issue), compose(size, ranges)) %>%
unlist()
# output dimensionality for the embedding layers, want +1 as a result of Python is 0-based
n_levels_out <- n_levels_in %>% sqrt() %>% trunc() %>% `+`(1)
# every embedding layer will get its personal enter layer
cat_inputs <- map(n_levels_in, operate(l) layer_input(form = 1)) %>%
unname()
# assemble the embedding layers, connecting every to its enter
embedding_layers <- vector(mode = "record", size = size(cat_inputs))
for (i in 1:size(cat_inputs)) {
embedding_layer <- cat_inputs[[i]] %>%
layer_embedding(input_dim = n_levels_in[[i]] + 1, output_dim = n_levels_out[[i]]) %>%
layer_flatten()
embedding_layers[[i]] <- embedding_layer
}In case you had been questioning concerning the flatten layer following every embedding: We have to squeeze out the third dimension (launched by the embedding layers) from the tensors, successfully rendering them rank-2.
That’s as a result of we wish to mix them with the rank-2 tensor popping out of the dense layer processing the numeric options.
So as to have the ability to mix it with something, we’ve to truly assemble that dense layer first. Will probably be linked to a single enter layer, of form 43, that takes within the numeric options we scaled in addition to the binary options we left untouched:
# create a single enter and a dense layer for the numeric information
quant_input <- layer_input(form = 43)
quant_dense <- quant_input %>% layer_dense(items = 64)Are components assembled, we wire them collectively utilizing layer_concatenate, and we’re good to name keras_model to create the ultimate graph.
intermediate_layers <- record(embedding_layers, record(quant_dense)) %>% flatten()
inputs <- record(cat_inputs, record(quant_input)) %>% flatten()
l <- 0.25
output <- layer_concatenate(intermediate_layers) %>%
layer_dense(items = 30, activation = "relu", kernel_regularizer = regularizer_l2(l)) %>%
layer_dropout(charge = 0.25) %>%
layer_dense(items = 10, activation = "relu", kernel_regularizer = regularizer_l2(l)) %>%
layer_dropout(charge = 0.25) %>%
layer_dense(items = 5, activation = "relu", kernel_regularizer = regularizer_l2(l)) %>%
layer_dropout(charge = 0.25) %>%
layer_dense(items = 1, activation = "sigmoid", kernel_regularizer = regularizer_l2(l))
mannequin <- keras_model(inputs, output)Now, should you’ve really learn by the entire of this half, you might want for a neater solution to get so far. So let’s swap to characteristic specs for the remainder of this put up.
Characteristic specs to the rescue
In spirit, the way in which characteristic specs are outlined follows the instance of the recipes bundle. (It gained’t make you hungry, although.) You initialize a characteristic spec with the prediction goal – feature_spec(goal ~ .), after which use the %>% to inform it what to do with particular person columns. “What to do” right here signifies two issues:
- First, easy methods to “learn in” the info. Are they numeric or categorical, and if categorical, what am I alleged to do with them? For instance, ought to I deal with all distinct symbols as distinct, leading to, probably, an infinite depend of classes – or ought to I constrain myself to a hard and fast variety of entities? Or hash them, even?
- Second, non-compulsory subsequent transformations. Numeric columns could also be bucketized; categorical columns could also be embedded. Or options may very well be mixed to seize interplay.
On this put up, we show the usage of a subset of step_ capabilities. The vignettes on Characteristic columns and Characteristic specs illustrate extra capabilities and their software.
Ranging from the start once more, right here is the entire code for information read-in and train-test break up within the characteristic spec model.
Information-prep-wise, recall what our targets are: depart alone if binary; scale if numeric; embed if categorical.
Specifying all of this doesn’t want quite a lot of strains of code:
Be aware how right here we’re passing within the coaching set, and similar to with recipes, we gained’t must repeat any of the steps for the validation set. Scaling is taken care of by scaler_standard(), an non-compulsory transformation operate handed in to step_numeric_column.
Categorical columns are supposed to make use of the entire vocabulary and pipe their outputs into embedding layers.
Now, what really occurred once we known as match()? So much – for us, as we removed a ton of guide preparation. For TensorFlow, nothing actually – it simply got here to learn about a couple of items within the graph we’ll ask it to assemble.
However wait, – don’t we nonetheless need to construct up that graph ourselves, connecting and concatenating layers?
Concretely, above, we needed to:
- create the right variety of enter layers, of appropriate form; and
- wire them to their matching embedding layers, of appropriate dimensionality.
So right here comes the actual magic, and it has two steps.
First, we simply create the enter layers by calling layer_input_from_dataset:
`
And second, we will extract the options from the characteristic spec and have layer_dense_features create the required layers based mostly on that data:
layer_dense_features(ft_spec$dense_features())With out additional ado, we add a couple of dense layers, and there may be our mannequin. Magic!
output <- inputs %>%
layer_dense_features(ft_spec$dense_features()) %>%
layer_dense(items = 30, activation = "relu", kernel_regularizer = regularizer_l2(l)) %>%
layer_dropout(charge = 0.25) %>%
layer_dense(items = 10, activation = "relu", kernel_regularizer = regularizer_l2(l)) %>%
layer_dropout(charge = 0.25) %>%
layer_dense(items = 5, activation = "relu", kernel_regularizer = regularizer_l2(l)) %>%
layer_dropout(charge = 0.25) %>%
layer_dense(items = 1, activation = "sigmoid", kernel_regularizer = regularizer_l2(l))
mannequin <- keras_model(inputs, output)How can we feed this mannequin? Within the non-feature-columns instance, we’d have needed to feed every enter individually, passing an inventory of tensors. Now we will simply go it the entire coaching set unexpectedly:
mannequin %>% match(x = coaching, y = coaching$goal)Within the Kaggle competitors, submissions are evaluated utilizing the normalized Gini coefficient, which we will calculate with the assistance of a brand new metric accessible in Keras, tf$keras$metrics$AUC(). For coaching, we will use an approximation to the AUC as a result of Yan et al. (2003) (Yan et al. 2003). Then coaching is as simple as:
auc <- tf$keras$metrics$AUC()
gini <- custom_metric(title = "gini", operate(y_true, y_pred) {
2*auc(y_true, y_pred) - 1
})
# Yan, L., Dodier, R., Mozer, M. C., & Wolniewicz, R. (2003).
# Optimizing Classifier Efficiency through an Approximation to the Wilcoxon-Mann-Whitney Statistic.
roc_auc_score <- operate(y_true, y_pred) {
pos = tf$boolean_mask(y_pred, tf$forged(y_true, tf$bool))
neg = tf$boolean_mask(y_pred, !tf$forged(y_true, tf$bool))
pos = tf$expand_dims(pos, 0L)
neg = tf$expand_dims(neg, 1L)
# authentic paper suggests efficiency is powerful to actual parameter selection
gamma = 0.2
p = 3
distinction = tf$zeros_like(pos * neg) + pos - neg - gamma
masked = tf$boolean_mask(distinction, distinction < 0.0)
tf$reduce_sum(tf$pow(-masked, p))
}
mannequin %>%
compile(
loss = roc_auc_score,
optimizer = optimizer_adam(),
metrics = record(auc, gini)
)
mannequin %>%
match(
x = coaching,
y = coaching$goal,
epochs = 50,
validation_data = record(testing, testing$goal),
batch_size = 512
)
predictions <- predict(mannequin, testing)
Metrics::auc(testing$goal, predictions)After 50 epochs, we obtain an AUC of 0.64 on the validation set, or equivalently, a Gini coefficient of 0.27. Not a nasty consequence for a easy totally linked community!
We’ve seen how utilizing characteristic columns automates away quite a few steps in organising the community, so we will spend extra time on really tuning it. That is most impressively demonstrated on a dataset like this, with greater than a handful categorical columns. Nevertheless, to clarify a bit extra what to concentrate to when utilizing characteristic columns, it’s higher to decide on a smaller instance the place we will simply do some peeking round.
Let’s transfer on to the second software.
Interactions, and what to look out for
To show the usage of step_crossed_column to seize interactions, we make use of the rugged dataset from Richard McElreath’s rethinking bundle.
We wish to predict log GDP based mostly on terrain ruggedness, for quite a few nations (170, to be exact). Nevertheless, the impact of ruggedness is totally different in Africa versus different continents. Citing from Statistical Rethinking
It is smart that ruggedness is related to poorer nations, in many of the world. Rugged terrain means transport is troublesome. Which implies market entry is hampered. Which implies lowered gross home product. So the reversed relationship inside Africa is puzzling. Why ought to troublesome terrain be related to increased GDP per capita?
If this relationship is in any respect causal, it could be as a result of rugged areas of Africa had been protected towards the Atlantic and Indian Ocean slave trades. Slavers most well-liked to raid simply accessed settlements, with straightforward routes to the ocean. These areas that suffered underneath the slave commerce understandably proceed to undergo economically, lengthy after the decline of slave-trading markets. Nevertheless, an end result like GDP has many influences, and is moreover a wierd measure of financial exercise. So it’s laborious to make certain what’s occurring right here.
Whereas the causal state of affairs is troublesome, the purely technical one is definitely described: We wish to study an interplay. We may depend on the community discovering out by itself (on this case it in all probability will, if we simply give it sufficient parameters). But it surely’s a wonderful event to showcase the brand new step_crossed_column.
Loading the dataset, zooming in on the variables of curiosity, and normalizing them the way in which it’s completed in Rethinking, we’ve:
Observations: 170
Variables: 3
$ log_gdp <dbl> 0.8797119, 0.9647547, 1.1662705, 1.1044854, 0.9149038,…
$ rugged <dbl> 0.1383424702, 0.5525636891, 0.1239922606, 0.1249596904…
$ africa <int> 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, …Now, let’s first overlook concerning the interplay and do the very minimal factor required to work with this information.
rugged needs to be a numeric column, whereas africa is categorical in nature, which implies we use one of many step_categorical_[...] capabilities on it. (On this case we occur to know there are simply two classes, Africa and not-Africa, so we may as nicely deal with the column as numeric like within the earlier instance; however in different purposes that gained’t be the case, so right here we present a technique that generalizes to categorical options on the whole.)
So we begin out making a characteristic spec and including the 2 predictor columns. We verify the consequence utilizing feature_spec’s dense_features() methodology:
$rugged
NumericColumn(key='rugged', form=(1,), default_value=None, dtype=tf.float32, normalizer_fn=None)Hm, that doesn’t look too good. The place’d africa go? In truth, there may be yet another factor we should always have completed: convert the explicit column to an indicator column. Why?
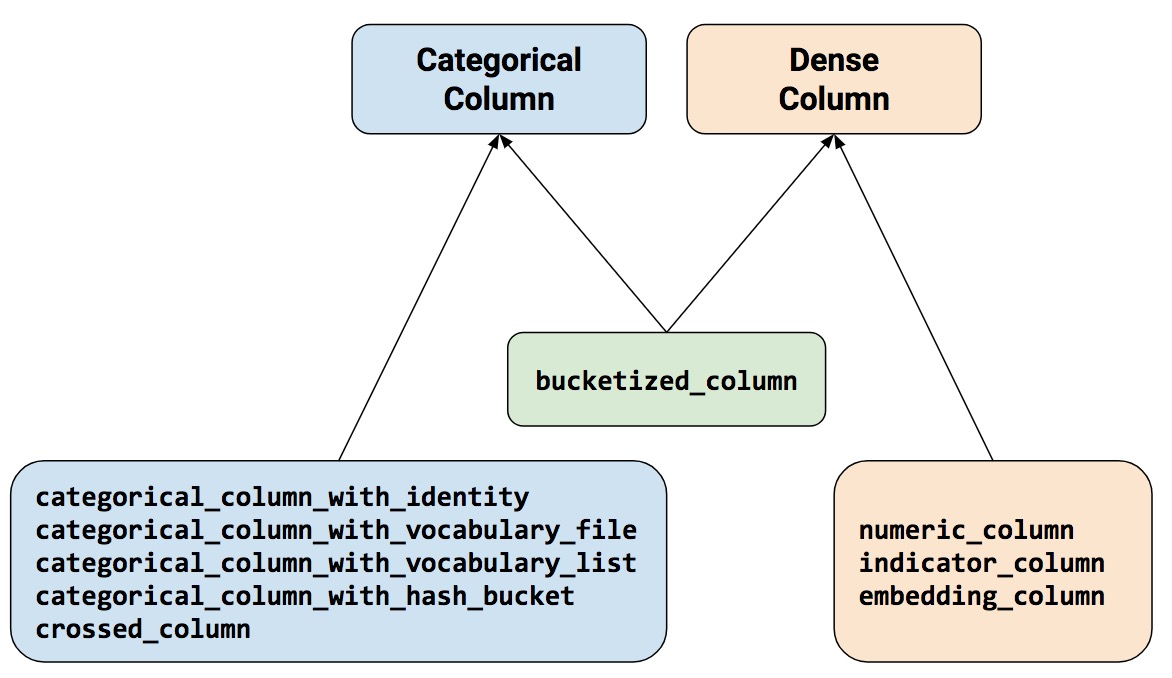
The rule of thumb is, each time you could have one thing categorical, together with crossed, that you must then rework it into one thing numeric, which incorporates indicator and embedding.
Being a heuristic, this rule works general, and it matches our instinct. There’s one exception although, step_bucketized_column, which though it “feels” categorical really doesn’t want that conversion.
Due to this fact, it’s best to complement that instinct with a easy lookup diagram, which can be a part of the characteristic columns vignette.
With this diagram, the easy rule is: We at all times want to finish up with one thing that inherits from DenseColumn. So:
step_numeric_column,step_indicator_column, andstep_embedding_columnare standalone;step_bucketized_columnis, too, nonetheless categorical it “feels”; and- all
step_categorical_column_[...], in addition tostep_crossed_column, must be remodeled utilizing one the dense column sorts.

Determine 1: To be used with Keras, all options want to finish up inheriting from DenseColumn by some means.
Thus, we will repair the state of affairs like so:
and now ft_spec$dense_features() will present us
$rugged
NumericColumn(key='rugged', form=(1,), default_value=None, dtype=tf.float32, normalizer_fn=None)
$indicator_africa
IndicatorColumn(categorical_column=IdentityCategoricalColumn(key='africa', number_buckets=2.0, default_value=None))
What we actually wished to do is seize the interplay between ruggedness and continent. To this finish, we first bucketize rugged, after which cross it with – already binary – africa. As per the principles, we lastly rework into an indicator column:
ft_spec <- coaching %>%
feature_spec(log_gdp ~ .) %>%
step_numeric_column(rugged) %>%
step_categorical_column_with_identity(africa, num_buckets = 2) %>%
step_indicator_column(africa) %>%
step_bucketized_column(rugged,
boundaries = c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8)) %>%
step_crossed_column(africa_rugged_interact = c(africa, bucketized_rugged),
hash_bucket_size = 16) %>%
step_indicator_column(africa_rugged_interact) %>%
match() this code you might be asking your self, now what number of options do I’ve within the mannequin?
Let’s verify.
$rugged
NumericColumn(key='rugged', form=(1,), default_value=None, dtype=tf.float32, normalizer_fn=None)
$indicator_africa
IndicatorColumn(categorical_column=IdentityCategoricalColumn(key='africa', number_buckets=2.0, default_value=None))
$bucketized_rugged
BucketizedColumn(source_column=NumericColumn(key='rugged', form=(1,), default_value=None, dtype=tf.float32, normalizer_fn=None), boundaries=(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8))
$indicator_africa_rugged_interact
IndicatorColumn(categorical_column=CrossedColumn(keys=(IdentityCategoricalColumn(key='africa', number_buckets=2.0, default_value=None), BucketizedColumn(source_column=NumericColumn(key='rugged', form=(1,), default_value=None, dtype=tf.float32, normalizer_fn=None), boundaries=(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8))), hash_bucket_size=16.0, hash_key=None))We see that every one options, authentic or remodeled, are saved, so long as they inherit from DenseColumn.
Which means, for instance, the non-bucketized, steady values of rugged are used as nicely.
Now organising the coaching goes as anticipated.
inputs <- layer_input_from_dataset(df %>% choose(-log_gdp))
output <- inputs %>%
layer_dense_features(ft_spec$dense_features()) %>%
layer_dense(items = 8, activation = "relu") %>%
layer_dense(items = 8, activation = "relu") %>%
layer_dense(items = 1)
mannequin <- keras_model(inputs, output)
mannequin %>% compile(loss = "mse", optimizer = "adam", metrics = "mse")
historical past <- mannequin %>% match(
x = coaching,
y = coaching$log_gdp,
validation_data = record(testing, testing$log_gdp),
epochs = 100)Simply as a sanity verify, the ultimate loss on the validation set for this code was ~ 0.014. However actually this instance did serve totally different functions.
In a nutshell
Characteristic specs are a handy, elegant method of creating categorical information accessible to Keras, in addition to to chain helpful transformations like bucketizing and creating crossed columns. The time you save information wrangling could go into tuning and experimentation. Take pleasure in, and thanks for studying!
Yan, Lian, Robert H Dodier, Michael Mozer, and Richard H Wolniewicz. 2003. “Optimizing Classifier Efficiency through an Approximation to the Wilcoxon-Mann-Whitney Statistic.” In Proceedings of the twentieth Worldwide Convention on Machine Studying (ICML-03), 848–55.