LoRA (Low-Rank Adaptation) is a brand new approach for positive tuning giant scale pre-trained
fashions. Such fashions are often educated on basic area knowledge, in order to have
the utmost quantity of knowledge. As a way to receive higher ends in duties like chatting
or query answering, these fashions could be additional ‘fine-tuned’ or tailored on area
particular knowledge.
It’s attainable to fine-tune a mannequin simply by initializing the mannequin with the pre-trained
weights and additional coaching on the area particular knowledge. With the rising measurement of
pre-trained fashions, a full ahead and backward cycle requires a considerable amount of computing
assets. Advantageous tuning by merely persevering with coaching additionally requires a full copy of all
parameters for every process/area that the mannequin is tailored to.
LoRA: Low-Rank Adaptation of Giant Language Fashions
proposes an answer for each issues through the use of a low rank matrix decomposition.
It might probably cut back the variety of trainable weights by 10,000 instances and GPU reminiscence necessities
by 3 instances.
Technique
The issue of fine-tuning a neural community could be expressed by discovering a (Delta Theta)
that minimizes (L(X, y; Theta_0 + DeltaTheta)) the place (L) is a loss perform, (X) and (y)
are the information and (Theta_0) the weights from a pre-trained mannequin.
We be taught the parameters (Delta Theta) with dimension (|Delta Theta|)
equals to (|Theta_0|). When (|Theta_0|) could be very giant, corresponding to in giant scale
pre-trained fashions, discovering (Delta Theta) turns into computationally difficult.
Additionally, for every process you’ll want to be taught a brand new (Delta Theta) parameter set, making
it much more difficult to deploy fine-tuned fashions when you have greater than a
few particular duties.
LoRA proposes utilizing an approximation (Delta Phi approx Delta Theta) with (|Delta Phi| << |Delta Theta|).
The commentary is that neural nets have many dense layers performing matrix multiplication,
and whereas they sometimes have full-rank throughout pre-training, when adapting to a selected process
the burden updates may have a low “intrinsic dimension”.
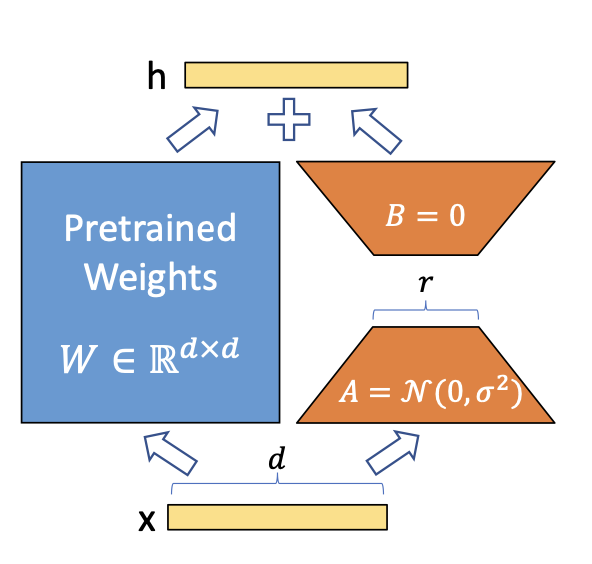
A easy matrix decomposition is utilized for every weight matrix replace (Delta theta in Delta Theta).
Contemplating (Delta theta_i in mathbb{R}^{d instances okay}) the replace for the (i)th weight
within the community, LoRA approximates it with:
[Delta theta_i approx Delta phi_i = BA]
the place (B in mathbb{R}^{d instances r}), (A in mathbb{R}^{r instances d}) and the rank (r << min(d, okay)).
Thus as an alternative of studying (d instances okay) parameters we now must be taught ((d + okay) instances r) which is well
lots smaller given the multiplicative facet. In apply, (Delta theta_i) is scaled
by (frac{alpha}{r}) earlier than being added to (theta_i), which could be interpreted as a
‘studying charge’ for the LoRA replace.
LoRA doesn’t improve inference latency, as as soon as positive tuning is completed, you possibly can merely
replace the weights in (Theta) by including their respective (Delta theta approx Delta phi).
It additionally makes it easier to deploy a number of process particular fashions on prime of 1 giant mannequin,
as (|Delta Phi|) is way smaller than (|Delta Theta|).
Implementing in torch
Now that we have now an concept of how LoRA works, let’s implement it utilizing torch for a
minimal downside. Our plan is the next:
- Simulate coaching knowledge utilizing a easy (y = X theta) mannequin. (theta in mathbb{R}^{1001, 1000}).
- Prepare a full rank linear mannequin to estimate (theta) – this will probably be our ‘pre-trained’ mannequin.
- Simulate a distinct distribution by making use of a change in (theta).
- Prepare a low rank mannequin utilizing the pre=educated weights.
Let’s begin by simulating the coaching knowledge:
We now outline our base mannequin:
mannequin <- nn_linear(d_in, d_out, bias = FALSE)We additionally outline a perform for coaching a mannequin, which we’re additionally reusing later.
The perform does the usual traning loop in torch utilizing the Adam optimizer.
The mannequin weights are up to date in-place.
practice <- perform(mannequin, X, y, batch_size = 128, epochs = 100) {
choose <- optim_adam(mannequin$parameters)
for (epoch in 1:epochs) {
for(i in seq_len(n/batch_size)) {
idx <- pattern.int(n, measurement = batch_size)
loss <- nnf_mse_loss(mannequin(X[idx,]), y[idx])
with_no_grad({
choose$zero_grad()
loss$backward()
choose$step()
})
}
if (epoch %% 10 == 0) {
with_no_grad({
loss <- nnf_mse_loss(mannequin(X), y)
})
cat("[", epoch, "] Loss:", loss$merchandise(), "n")
}
}
}The mannequin is then educated:
practice(mannequin, X, y)
#> [ 10 ] Loss: 577.075
#> [ 20 ] Loss: 312.2
#> [ 30 ] Loss: 155.055
#> [ 40 ] Loss: 68.49202
#> [ 50 ] Loss: 25.68243
#> [ 60 ] Loss: 7.620944
#> [ 70 ] Loss: 1.607114
#> [ 80 ] Loss: 0.2077137
#> [ 90 ] Loss: 0.01392935
#> [ 100 ] Loss: 0.0004785107OK, so now we have now our pre-trained base mannequin. Let’s suppose that we have now knowledge from
a slighly totally different distribution that we simulate utilizing:
thetas2 <- thetas + 1
X2 <- torch_randn(n, d_in)
y2 <- torch_matmul(X2, thetas2)If we apply out base mannequin to this distribution, we don’t get an excellent efficiency:
nnf_mse_loss(mannequin(X2), y2)
#> torch_tensor
#> 992.673
#> [ CPUFloatType{} ][ grad_fn = <MseLossBackward0> ]We now fine-tune our preliminary mannequin. The distribution of the brand new knowledge is simply slighly
totally different from the preliminary one. It’s only a rotation of the information factors, by including 1
to all thetas. Because of this the burden updates are usually not anticipated to be complicated, and
we shouldn’t want a full-rank replace with a purpose to get good outcomes.
Let’s outline a brand new torch module that implements the LoRA logic:
lora_nn_linear <- nn_module(
initialize = perform(linear, r = 16, alpha = 1) {
self$linear <- linear
# parameters from the unique linear module are 'freezed', so they aren't
# tracked by autograd. They're thought-about simply constants.
purrr::stroll(self$linear$parameters, (x) x$requires_grad_(FALSE))
# the low rank parameters that will probably be educated
self$A <- nn_parameter(torch_randn(linear$in_features, r))
self$B <- nn_parameter(torch_zeros(r, linear$out_feature))
# the scaling fixed
self$scaling <- alpha / r
},
ahead = perform(x) {
# the modified ahead, that simply provides the end result from the bottom mannequin
# and ABx.
self$linear(x) + torch_matmul(x, torch_matmul(self$A, self$B)*self$scaling)
}
)We now initialize the LoRA mannequin. We are going to use (r = 1), that means that A and B will probably be simply
vectors. The bottom mannequin has 1001×1000 trainable parameters. The LoRA mannequin that we’re
are going to positive tune has simply (1001 + 1000) which makes it 1/500 of the bottom mannequin
parameters.
lora <- lora_nn_linear(mannequin, r = 1)Now let’s practice the lora mannequin on the brand new distribution:
practice(lora, X2, Y2)
#> [ 10 ] Loss: 798.6073
#> [ 20 ] Loss: 485.8804
#> [ 30 ] Loss: 257.3518
#> [ 40 ] Loss: 118.4895
#> [ 50 ] Loss: 46.34769
#> [ 60 ] Loss: 14.46207
#> [ 70 ] Loss: 3.185689
#> [ 80 ] Loss: 0.4264134
#> [ 90 ] Loss: 0.02732975
#> [ 100 ] Loss: 0.001300132 If we take a look at (Delta theta) we are going to see a matrix stuffed with 1s, the precise transformation
that we utilized to the weights:
delta_theta <- torch_matmul(lora$A, lora$B)*lora$scaling
delta_theta[1:5, 1:5]
#> torch_tensor
#> 1.0002 1.0001 1.0001 1.0001 1.0001
#> 1.0011 1.0010 1.0011 1.0011 1.0011
#> 0.9999 0.9999 0.9999 0.9999 0.9999
#> 1.0015 1.0014 1.0014 1.0014 1.0014
#> 1.0008 1.0008 1.0008 1.0008 1.0008
#> [ CPUFloatType{5,5} ][ grad_fn = <SliceBackward0> ]To keep away from the extra inference latency of the separate computation of the deltas,
we may modify the unique mannequin by including the estimated deltas to its parameters.
We use the add_ technique to switch the burden in-place.
with_no_grad({
mannequin$weight$add_(delta_theta$t())
})Now, making use of the bottom mannequin to knowledge from the brand new distribution yields good efficiency,
so we will say the mannequin is tailored for the brand new process.
nnf_mse_loss(mannequin(X2), y2)
#> torch_tensor
#> 0.00130013
#> [ CPUFloatType{} ]Concluding
Now that we discovered how LoRA works for this easy instance we will assume the way it may
work on giant pre-trained fashions.
Seems that Transformers fashions are largely intelligent group of those matrix
multiplications, and making use of LoRA solely to those layers is sufficient for lowering the
positive tuning value by a big quantity whereas nonetheless getting good efficiency. You possibly can see
the experiments within the LoRA paper.
In fact, the concept of LoRA is straightforward sufficient that it may be utilized not solely to
linear layers. You possibly can apply it to convolutions, embedding layers and truly another layer.
Picture by Hu et al on the LoRA paper
