[Image by Author]
The idea of “function significance” is broadly utilized in machine studying as essentially the most fundamental sort of mannequin explainability. For instance, it’s utilized in Recursive Function Elimination (RFE), to iteratively drop the least vital function of the mannequin.
Nonetheless, there’s a false impression about it.
The truth that a function is vital doesn’t suggest that it’s useful for the mannequin!
Certainly, after we say {that a} function is vital, this merely implies that the function brings a excessive contribution to the predictions made by the mannequin. However we should always take into account that such contribution could also be incorrect.
Take a easy instance: an information scientist by chance forgets the Buyer ID between its mannequin’s options. The mannequin makes use of Buyer ID as a extremely predictive function. As a consequence, this function could have a excessive function significance even whether it is truly worsening the mannequin, as a result of it can’t work effectively on unseen knowledge.
To make issues clearer, we might want to make a distinction between two ideas:
- Prediction Contribution: what a part of the predictions is as a result of function; that is equal to function significance.
- Error Contribution: what a part of the prediction errors is as a result of presence of the function within the mannequin.
On this article, we’ll see the right way to calculate these portions and the right way to use them to get beneficial insights a couple of predictive mannequin (and to enhance it).
Notice: this text is concentrated on the regression case. If you’re extra within the classification case, you possibly can learn “Which options are dangerous in your classification mannequin?”
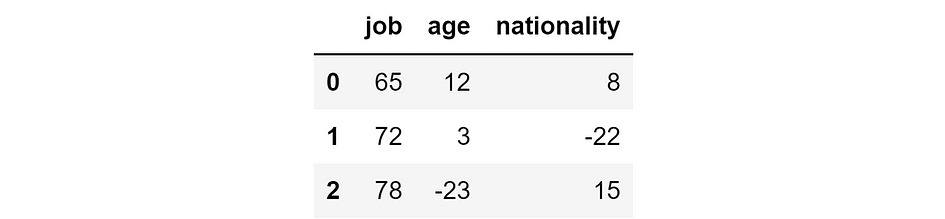
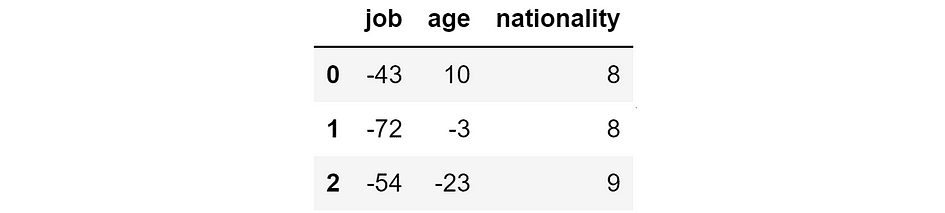
Suppose we constructed a mannequin to foretell the earnings of individuals based mostly on their job, age, and nationality. Now we use the mannequin to make predictions on three folks.
Thus, we’ve got the bottom reality, the mannequin prediction, and the ensuing error:

Floor reality, mannequin prediction, and absolute error (in hundreds of $). [Image by Author]
When we’ve got a predictive mannequin, we are able to all the time decompose the mannequin predictions into the contributions introduced by the one options. This may be completed by way of SHAP values (should you don’t find out about how SHAP values work, you possibly can learn my article: SHAP Values Defined Precisely How You Wished Somebody Defined to You).
So, let’s say these are the SHAP values relative to our mannequin for the three people.
SHAP values for our mannequin’s predictions (in hundreds of $). [Image by Author]
The principle property of SHAP values is that they’re additive. Because of this — by taking the sum of every row — we’ll acquire our mannequin’s prediction for that particular person. As an illustration, if we take the second row: 72k $ +3k $ -22k $ = 53k $, which is precisely the mannequin’s prediction for the second particular person.
Now, SHAP values are a great indicator of how vital a function is for our predictions. Certainly, the upper the (absolute) SHAP worth, the extra influential the function for the prediction about that particular particular person. Notice that I’m speaking about absolute SHAP values as a result of the signal right here doesn’t matter: a function is equally vital if it pushes the prediction up or down.
Subsequently, the Prediction Contribution of a function is the same as the imply of absolutely the SHAP values of that function. When you have the SHAP values saved in a Pandas dataframe, this is so simple as:
prediction_contribution = shap_values.abs().imply()
In our instance, that is the outcome:

Prediction Contribution. [Image by Author]
As you possibly can see, job is clearly a very powerful function since, on common, it accounts for 71.67k $ of the ultimate prediction. Nationality and age are respectively the second and the third most related function.
Nonetheless, the truth that a given function accounts for a related a part of the ultimate prediction doesn’t inform something in regards to the function’s efficiency. To contemplate additionally this side, we might want to compute the “Error Contribution”.
Let’s say that we wish to reply the next query: “What predictions would the mannequin make if it didn’t have the function job?” SHAP values permit us to reply this query. In actual fact, since they’re additive, it’s sufficient to subtract the SHAP values relative to the function job from the predictions made by the mannequin.
In fact, we are able to repeat this process for every function. In Pandas:
y_pred_wo_feature = shap_values.apply(lambda function: y_pred - function)
That is the result:
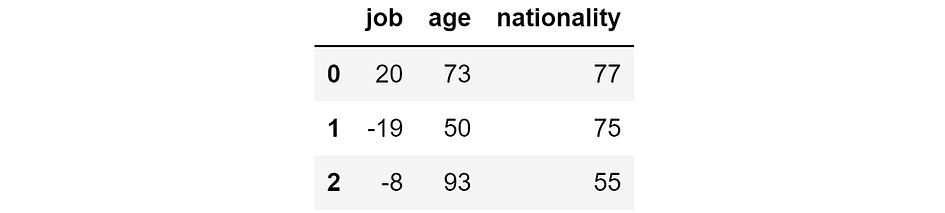
Predictions that we’d acquire if we eliminated the respective function. [Image by Author]
Because of this, if we didn’t have the function job, then the mannequin would predict 20k $ for the primary particular person, -19k $ for the second, and -8k $ for the third one. As a substitute, if we didn’t have the function age, the mannequin would predict 73k $ for the primary particular person, 50k $ for the second, and so forth.
As you possibly can see, the predictions for every particular person range lots if we eliminated totally different options. As a consequence, additionally the prediction errors can be very totally different. We will simply compute them:
abs_error_wo_feature = y_pred_wo_feature.apply(lambda function: (y_true - function).abs())
The result’s the next:
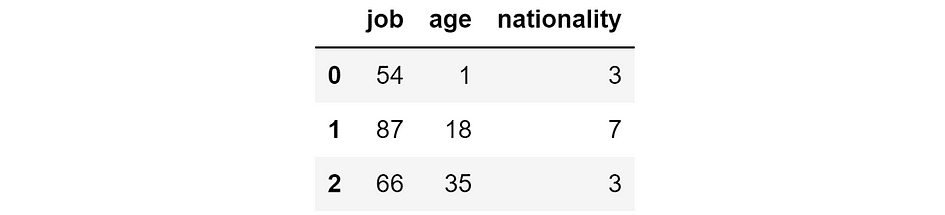
Absolute errors that we’d acquire if we eliminated the respective function. [Image by Author]
These are the errors that we’d acquire if we eliminated the respective function. Intuitively, if the error is small, then eradicating the function is just not an issue — or it’s even useful — for the mannequin. If the error is excessive, then eradicating the function is just not a good suggestion.
However we are able to do greater than this. Certainly, we are able to compute the distinction between the errors of the complete mannequin and the errors we’d acquire with out the function:
error_diff = abs_error_wo_feature.apply(lambda function: abs_error - function)
Which is:
Distinction between the errors of the mannequin and the errors we’d have with out the function. [Image by Author]
If this quantity is:
- adverse, then the presence of the function results in a discount within the prediction error, so the function works effectively for that commentary!
- constructive, then the presence of the function results in a rise within the prediction error, so the function is unhealthy for that commentary.
We will compute “Error Contribution” because the imply of those values, for every function. In Pandas:
error_contribution = error_diff.imply()
That is the result:

Error Contribution. [Image by Author]
If this worth is constructive, then it implies that, on common, the presence of the function within the mannequin results in the next error. Thus, with out that function, the prediction would have been usually higher. In different phrases, the function is making extra hurt than good!
Quite the opposite, the extra adverse this worth, the extra useful the function is for the predictions since its presence results in smaller errors.
Let’s attempt to use these ideas on an actual dataset.
Hereafter, I’ll use a dataset taken from Pycaret (a Python library below MIT license). The dataset is known as “Gold” and it comprises time collection of economic knowledge.
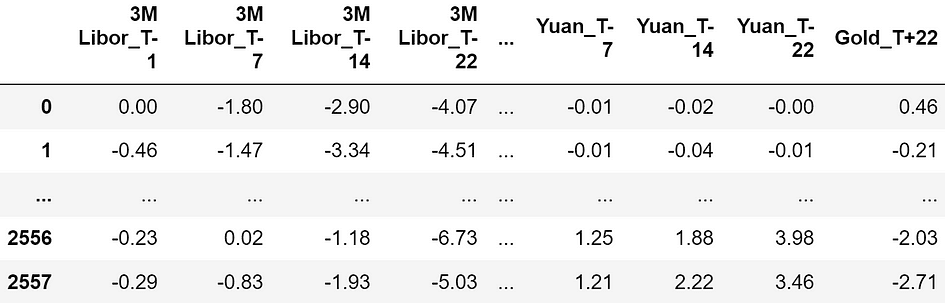
Dataset pattern. The options are all expressed in proportion, so -4.07 means a return of -4.07%. [Image by Author]
The options consist within the returns of economic belongings respectively 22, 14, 7, and 1 days earlier than the commentary second (“T-22”, “T-14”, “T-7”, “T-1”). Right here is the exhaustive listing of all of the monetary belongings used as predictive options:

Listing of the out there belongings. Every asset is noticed at time -22, -14, -7, and -1. [Image by Author]
In complete, we’ve got 120 options.
The aim is to foretell the Gold worth (return) 22 days forward in time (“Gold_T+22”). Let’s check out the goal variable.
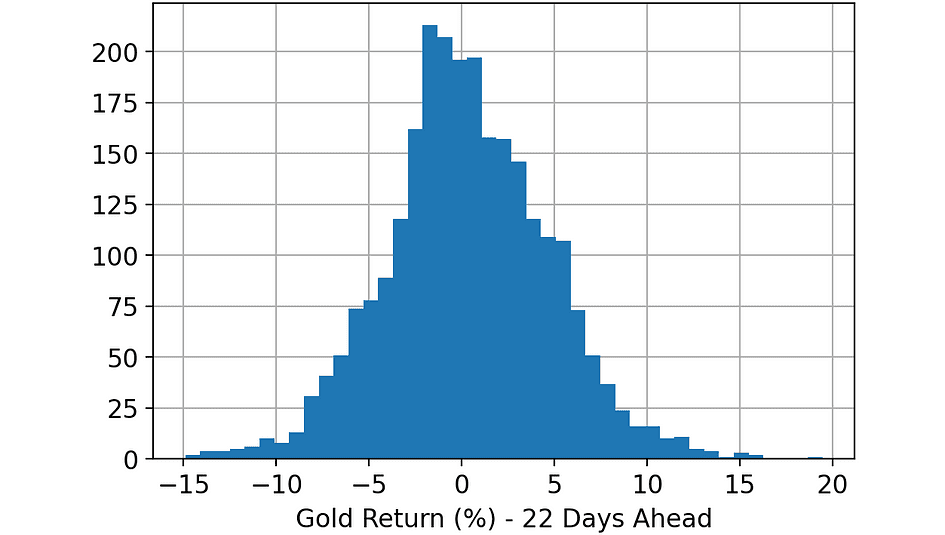
Histogram of the variable. [Image by Author]
As soon as I loaded the dataset, these are the steps I carried out:
- Cut up the complete dataset randomly: 33% of the rows within the coaching dataset, one other 33% within the validation dataset, and the remaining 33% within the check dataset.
- Practice a LightGBM Regressor on the coaching dataset.
- Make predictions on coaching, validation, and check datasets, utilizing the mannequin educated on the earlier step.
- Compute SHAP values of coaching, validation, and check datasets, utilizing the Python library “shap”.
- Compute the Prediction Contribution and the Error Contribution of every function on every dataset (coaching, validation, and check), utilizing the code we’ve got seen within the earlier paragraph.
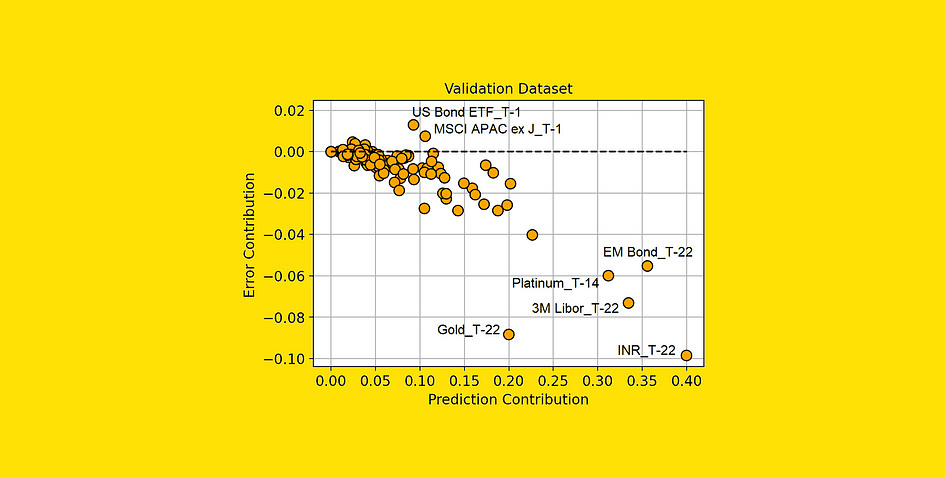
Let’s evaluate the Error Contribution and the Prediction Contribution within the coaching dataset. We are going to use a scatter plot, so the dots establish the 120 options of the mannequin.
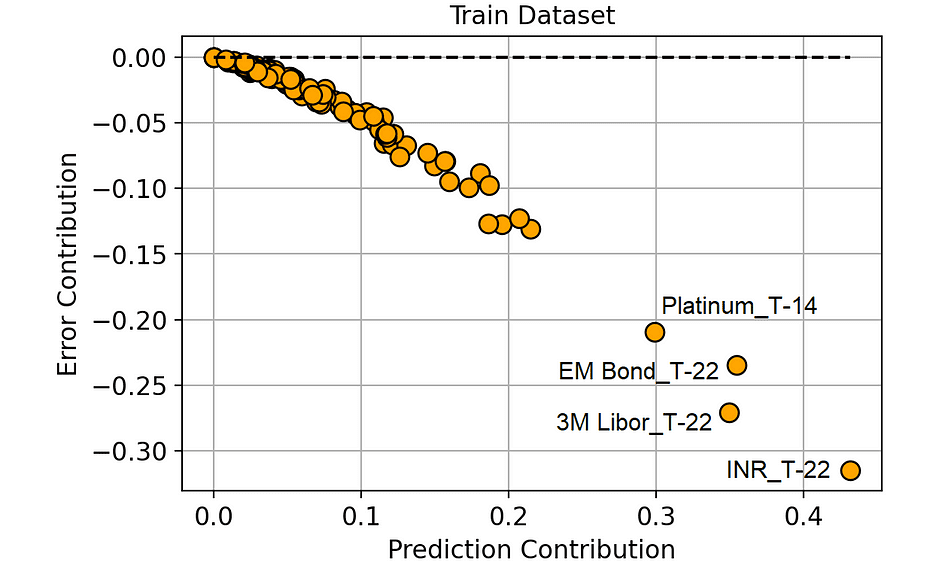
Prediction Contribution vs. Error Contribution (on the Coaching dataset). [Image by Author]
There’s a extremely adverse correlation between Prediction Contribution and Error Contribution within the coaching set.
And this is sensible: because the mannequin learns on the coaching dataset, it tends to attribute excessive significance (i.e. excessive Prediction Contribution) to these options that result in an amazing discount within the prediction error (i.e. extremely adverse Error Contribution).
However this doesn’t add a lot to our information, proper?
Certainly, what actually issues to us is the validation dataset. The validation dataset is in reality the perfect proxy we are able to have about how our options will behave on new knowledge. So, let’s make the identical comparability on the validation set.
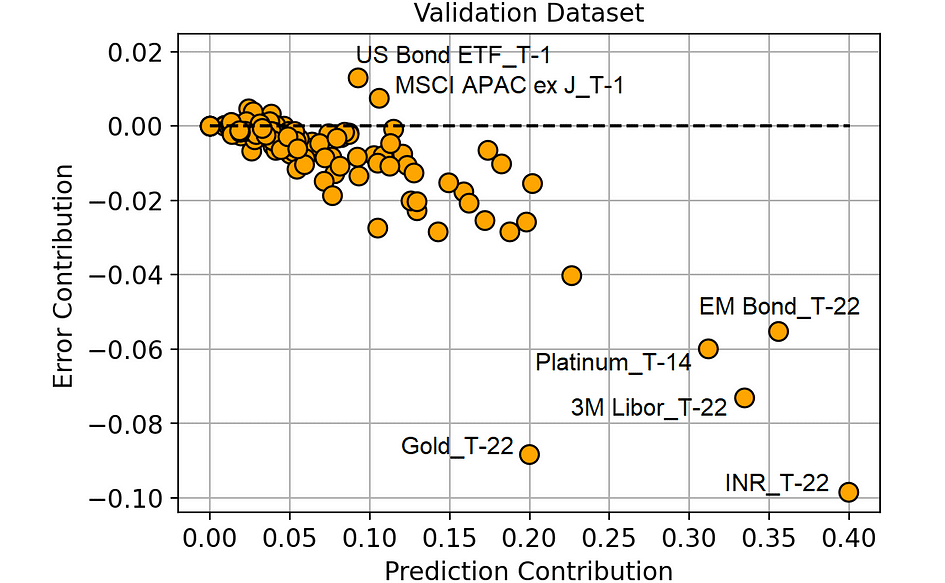
Prediction Contribution vs. Error Contribution (on the Validation dataset). [Image by Author]
From this plot, we are able to extract some far more fascinating data.
The options within the decrease proper a part of the plot are these to which our mannequin is appropriately assigning excessive significance since they really deliver a discount within the prediction error.
Additionally, notice that “Gold_T-22” (the return of gold 22 days earlier than the commentary interval) is working rather well in comparison with the significance that the mannequin is attributing to it. Because of this this function is probably underfitting. And this piece of data is especially fascinating since gold is the asset we are attempting to foretell (“Gold_T+22”).
However, the options which have an Error Contribution above 0 are making our predictions worse. As an illustration, “US Bond ETF_T-1” on common adjustments the mannequin prediction by 0.092% (Prediction Contribution), however it leads the mannequin to make a prediction on common 0.013% (Error Contribution) worse than it might have been with out that function.
We could suppose that all of the options with a excessive Error Contribution (in comparison with their Prediction Contribution) are most likely overfitting or, usually, they’ve totally different conduct within the coaching set and within the validation set.
Let’s see which options have the biggest Error Contribution.
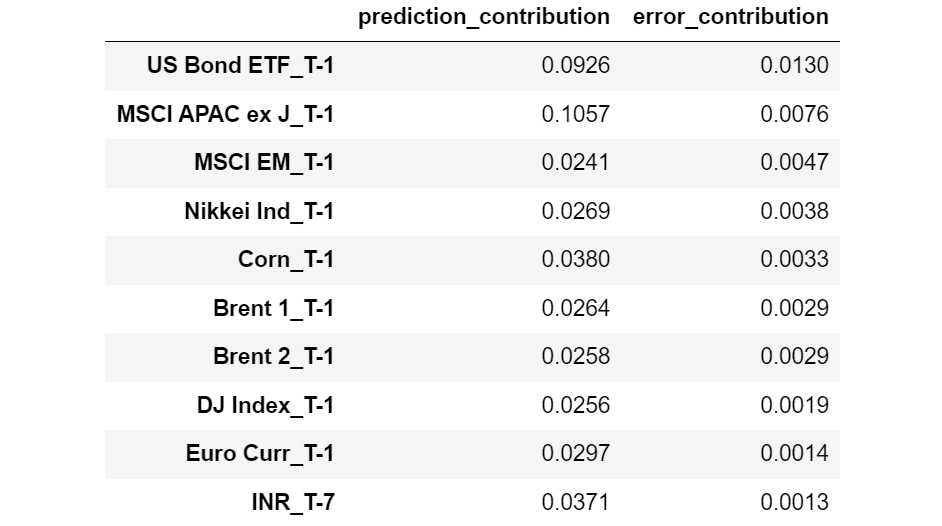
Options sorted by reducing Error Contribution. [Image by Author]
And now the options with the bottom Error Contribution:
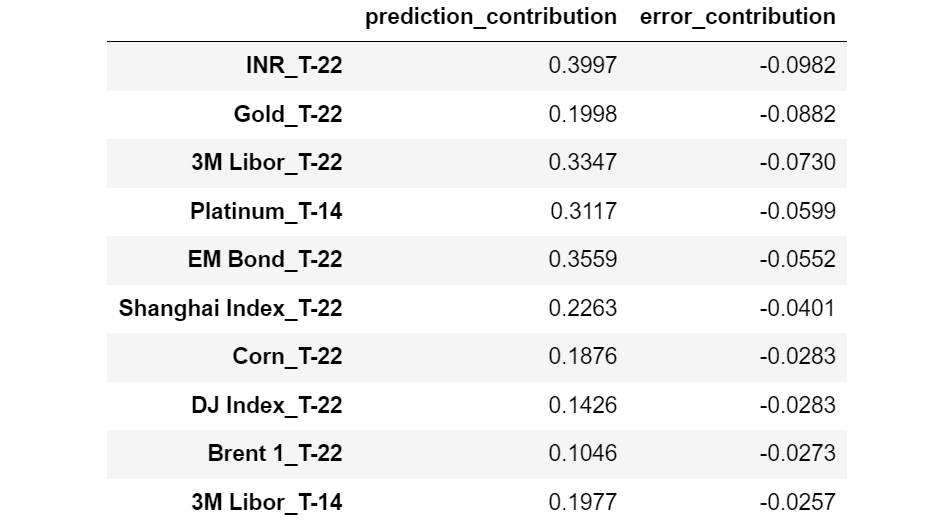
Options sorted by rising Error Contribution. [Image by Author]
Curiously, we could observe that every one the options with larger Error Contribution are relative to T-1 (1 day earlier than the commentary second), whereas virtually all of the options with smaller Error Contribution are relative to T-22 (22 days earlier than the commentary second).
This appears to point that the newest options are susceptible to overfitting, whereas the options extra distant in time are likely to generalize higher.
Notice that, with out Error Contribution, we’d by no means have recognized this perception.
Conventional Recursive Function Elimination (RFE) strategies are based mostly on the removing of unimportant options. That is equal to eradicating the options with a small Prediction Contribution first.
Nonetheless, based mostly on what we stated within the earlier paragraph, it might make extra sense to take away the options with the very best Error Contribution first.
To examine whether or not our instinct is verified, let’s evaluate the 2 approaches:
- Conventional RFE: eradicating ineffective options first (lowest Prediction Contribution).
- Our RFE: eradicating dangerous options first (highest Error Contribution).
Let’s see the outcomes on the validation set:
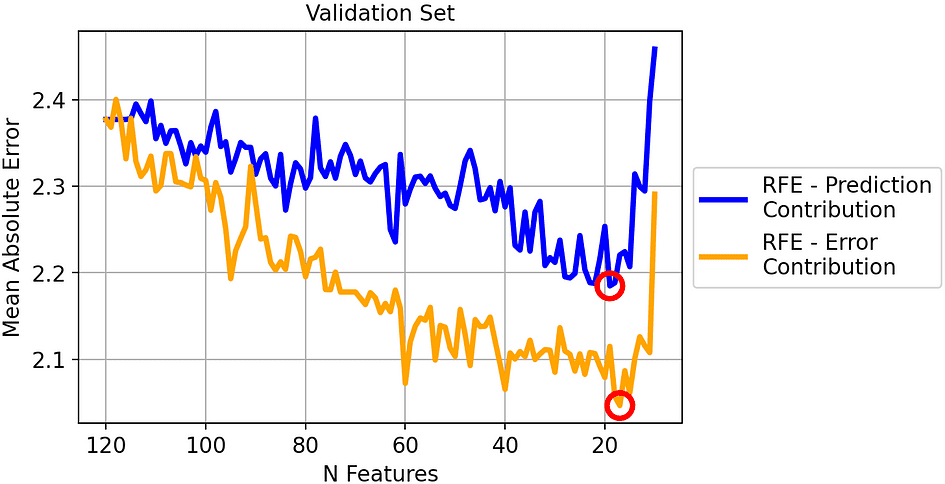
Imply Absolute Error of the 2 methods on the validation set. [Image by Author]
The most effective iteration for every technique has been circled: it’s the mannequin with 19 options for the standard RFE (blue line) and the mannequin with 17 options for our RFE (orange line).
Basically, evidently our technique works effectively: eradicating the function with the very best Error Contribution results in a persistently smaller MAE in comparison with eradicating the function with the very best Prediction Contribution.
Nonetheless, you might suppose that this works effectively simply because we’re overfitting the validation set. In any case, we have an interest within the outcome that we’ll acquire on the check set.
So let’s see the identical comparability on the check set.
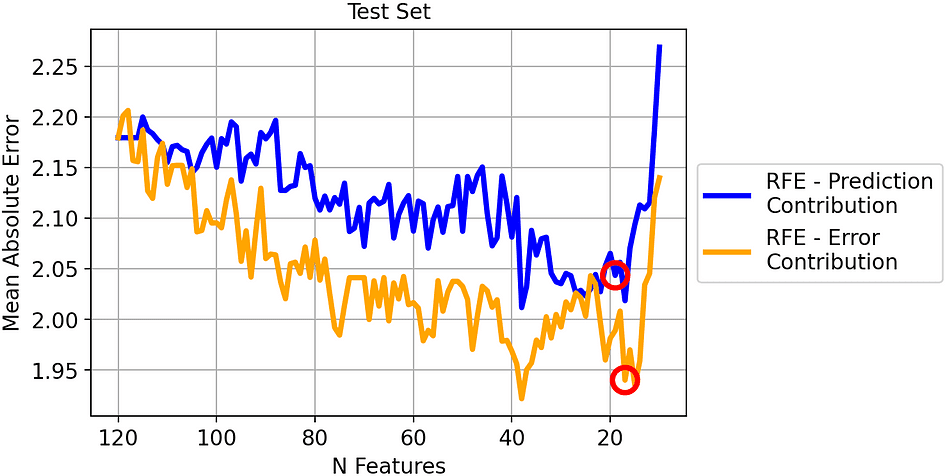
Imply Absolute Error of the 2 methods on the check set. [Image by Author]
The result’s just like the earlier one. Even when there may be much less distance between the 2 traces, the MAE obtained by eradicating the very best Error Contributor is clearly higher than the MAE by obtained eradicating the bottom Prediction Contributor.
Since we chosen the fashions resulting in the smallest MAE on the validation set, let’s see their final result on the check set:
- RFE-Prediction Contribution (19 options). MAE on check set: 2.04.
- RFE-Error Contribution (17 options). MAE on check set: 1.94.
So the perfect MAE utilizing our technique is 5% higher in comparison with conventional RFE!
The idea of function significance performs a basic function in machine studying. Nonetheless, the notion of “significance” is usually mistaken for “goodness”.
With a view to distinguish between these two elements we’ve got launched two ideas: Prediction Contribution and Error Contribution. Each ideas are based mostly on the SHAP values of the validation dataset, and within the article we’ve got seen the Python code to compute them.
We’ve got additionally tried them on an actual monetary dataset (wherein the duty is predicting the value of Gold) and proved that Recursive Function Elimination based mostly on Error Contribution results in a 5% higher Imply Absolute Error in comparison with conventional RFE based mostly on Prediction Contribution.
All of the code used for this text may be present in this pocket book.
Thanks for studying!
Samuele Mazzanti is Lead Information Scientist at Jakala and presently lives in Rome. He graduated in Statistics and his important analysis pursuits concern machine studying functions for the business. He’s additionally a contract content material creator.
Authentic. Reposted with permission.
